SIFT-MS Analytic Method

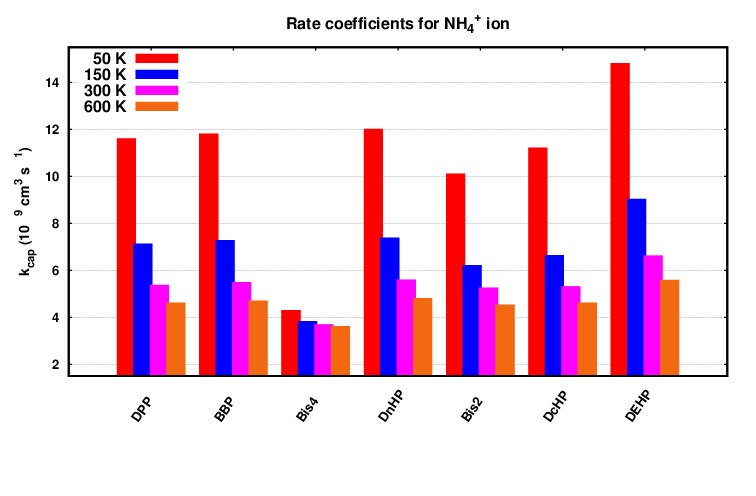
These Direct Injection Mass Spectrometry (DIMS) techniques rely on calibrating instruments using standards with known concentrations and protonated ion signals. Although the most accurate analysis requires calibrating the instrument for each volatile organic compound (VOC) in a complex gas mixture, this process is both labor-intensive and time-consuming. In practice, obtaining precise standards for every detected VOC is often impractical. Alternatively, VOC concentrations in Proton Transfer Reaction Mass Spectrometry (PTR-MS) can be determined by measuring the counts of protonated VOC ions (VOC.H⁺) and reagent ions (H₃O⁺). By utilizing the rate coefficient of the proton-transfer reaction, which depends on the reaction kinetics within PTR-MS or Selected Ion Flow Tube Mass Spectrometry (SIFT-MS) instruments, concentrations can be estimated. Su and colleagues have proposed several theoretical and numerical approaches for ion-molecule collision reactions, taking into account the molecular polarizability and electric dipole moment of the VOCs as input parameters.

Theoretical Models

The Langevin theory provides a detailed description of ion-molecule collision reactions involving non-polar molecules. In this model, the ion is simplified as a point charge, while the non-polar molecule is depicted as a point particle. The dominant factor in ion-nonpolar molecule interactions is the long-range ion-induced dipole interactions. The potential governing these ion-induced dipole interactions is expressed as: $$V(r) = -\frac{1}{4\pi \epsilon_0} \frac{\alpha {q^2}}{2r^4}\,,$$ where q=zq_e is the charge of the ion (q_e is the elementary charge in Coulomb); ɑ is the polarizability of the neutral species, and r is the distance between the centers of mass of the ion and neutral molecule. The rate coefficient can be obtained from the Langevin model as follows, $$ {\rm k}_{\rm Lang}=\sqrt{\frac{\pi \alpha q^{2}}{\mu_{\rm m} \epsilon_{0}}} \,,$$ where μ_m is the reduced mass of the reactants. Above equation anticipates rate coefficients for collisions between ions and non-polar molecules under high-temperature conditions, but the computed rates do not apply to polar molecules. Calculating ion-polar molecule collision rate coefficients using trajectory simulations involves modeling the paths of ions and polar molecules during collisions and analyzing the resulting collision frequencies and outcomes. Classical trajectory calculations simulate these paths as particles move through space and interact. Su and Chesnavich utilized trajectory calculations to enhance accuracy beyond the Langevin model, treating ions as point charges and polar molecules as two-dimensional rigid rotors. Su further refined this trajectory method, calculating rate coefficients over a wide temperature range using classical trajectory simulations. The resulting rate coefficients closely matched experimental data, demonstrating accuracy within a 3% margin. The trajectory model and the parameterized expression are described by the following equations: $$ \rm k_{\rm cap}( T)=\rm k_{\rm Lang} \, \it K_{\rm cap}(\rm T_R, {I}^{\star})\,.$$ The parameterized quantity K_cap(T_R, I^*) depends on two reduced parameters: the dimensionless reduced temperature T_R and the moment of inertia I^* of the neutral molecule. Here, $$ \rm T_{R}=4\pi\epsilon_{0} \frac{2\alpha k_{B}\rm T}{\mu_{\rm D}^2} $$ and the dimensionless parameter $$ \rm I^{\star}= \frac{\mu_{\rm D}\rm I}{\alpha \it q \mu_{\rm m}} \,.$$ I is the moment of inertia of the neutral molecule. Further solving the trajectories, Su and Chesnavich suggested that the value of K_cap is insensitive to I^* when $$ \rm I^{\star} < \frac{0.7+x^{2}}{2+0.6x} \,, $$ where $$ x= \rm T_{R}^{-1/2} \,. $$ For the molecular species studied in PTR-MS, the values of ɑ, μ_D and I are such that K_cap lies in the insensitive region because of the above inequality. Under such circumstances, K_cap depends only on T_R, i.e. on x, and its value is parameterized as follows:
$$ K_{\rm cap}=\begin{cases} ({x}+0.5090)^2/10.526+{0.9754}, & x \leq 2\\ 0.4767\,x+0.6200, & 2 < x \leq 3\\ 0.5781\,x+0.3165, & 3 < x \leq 35\\ 0.6201\,x-1.153, & 35 < x \leq 60\\ 0.6347\,x-2.029, & x < 60 \,. \end{cases} $$

Additional information regarding this theory can be found in the related literature. Given the challenges inherent in direct experimental determination, collision-based models are commonly utilized to determine rate coefficients. Direct experimental methods are often laborious, time-consuming, and susceptible to errors, potentially resulting in deviations of up to ±30%.

SIFT-MS utilizes a flow tube reactor where analyte molecules react with a mixture of reagent ions, such as H₃O⁺, O₂^+*, and NO⁺. The reactions lead to the formation of product ions, which are subsequently analyzed by mass spectrometry. SIFT-MS offers rapid analysis with high selectivity and sensitivity, making it suitable for online and real-time monitoring of VOCs in various applications, including industrial processes, environmental monitoring, and medical diagnostics. SIFT-MS, capable of swiftly alternating between different reagent ions, serves as a direct mass spectrometry technique with a typical detection limit as low as pptv. This method achieves real-time and quantitative analysis by employing precisely controlled soft chemical ionization (CI), thus obviating the need
for sample preparation, pre-concentration, and chromatography.