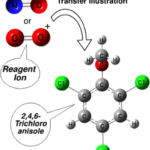
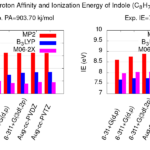
Energetics: PTR-MS Drift-tube Conditions

A commonly used ionization procedure in a classic PTR-MS instrument incorporates proton-transfer reactions, usually taking H₃O⁺ as a proton donor. One of the biggest benefit of using H₃O⁺ as promary reagent ion is that it does not react with most of the air constituents, as their proton affinity (PA) values are lower than that of H₂O. However, most of the VOCs fall in the range of having PAs larger than that of water, except smaller alkanes and ethenes. A proton transfer from H₃O⁺ is energetically possible if the PA of the analyte is higher than the PA of the water molecule. Generally, room-temperature rate coefficients are usually employed for quantitative analysis in PTR-MS. However, due to highly energetic reaction conditions inside the PTR-MS drift tube due to the applied electric field, the rate coefficients at thermal conditions cannot be used straight away due to the applied electric field. As a result, the translational energy of the colliding ions leads to the center-of-mass energy, which is higher than the energy under thermal conditions. Total mean ion kinetic energy of the ions in the drift tube is given as $$\rm KE_{\rm ion} = \frac{3}{2}{k_{\rm B} T}+\frac{1}{2}{m_{\rm ion} v_{\rm drift}^{2}}+\frac{1}{2}{\rm M_{\rm buffer}}v_{\rm drift}^{2},$$ where $m_{\rm ion}$ is mass of the ion, $v_{\rm drift}$ is drift velocity of the ion, and $\rm M_{\rm buffer}$ is mass of the buffer gas. $k_{\rm B}$ is the Boltzmann’s constant. The center-of-mass kinetic energy for an ion-neutral molecule collision is obtained by the following expression: $$\rm KE_{\rm com}=\frac{3}{2}k_{\rm B}T+\left ( \frac{\rm M_{N}}{m_{\rm ion}+\rm M_{N}}\right) \left( KE_{\rm ion}-\frac{3}{2}k_{\rm B}T \right) ,$$ Here, $\rm M_{N}$ represents the mass of the neutral molecule. Highly energetic conditions inside the drift tube lead to a relatively higher effective temperature, $rm T_{rm eff}$, for a collision in the PTR-MS drift tube. $rm T_{rm eff}$ can be obtained by equating an effective ion thermal energy with the mean center-of-mass collision energy between the ion and the buffer gas. The effective temperature $rm T_{rm eff}$ is obtained as $$\rm T_{\rm eff}= \rm T+ \left (\frac{v_{\rm drift}^2}{3k_{\rm B}} \right) \left [ \frac{\rm M_N ( m_{\rm ion}+\rm M_{buffer} ) }{m_{\rm ion}+\rm M_N} \right] \,.$$ Here $\rm T$ is the drift-tube temperature, and the remaining terms are as defined earlier.

  Under highly energetic conditions of the PTR-MS, the rate coefficients can be obtained by parameterized trajectory model as given by Su are considered appropriate at center-of-mass kinetic energy and higher effective temperature.

Rate Coefficients Calculation

There are a few different ways to compute rate coefficients in chemical ionization mass spectrometry (CI-MS). One common method is to use the capture collision model. This model assumes that the rate of reaction between a reagent ion and a neutral molecule is proportional to the relative velocity of the two species and the cross-section for the reaction. Pure polarization based method commonly called Langevin model, is used for computing rate coefficients in CI-MS.

The choice of which method to use for computing rate coefficients in CI-MS depends on the specific system being studied. The capture collision model is generally more accurate for reactions that occur at low collision energies, while the Langevin model is generally more accurate for reactions that occur at high collision energies.

The choice of which method to use for computing rate coefficients in CI-MS depends on the specific system being studied. The capture collision model is generally more accurate for reactions that occur at low collision energies, while the Langevin model is generally more accurate for reactions that occur at high collision energies.

The parameterized trajectory method is considered more accurate for calculating rate coefficients in proton transfer reaction mass spectrometry (PTR-MS) drift tube conditions.

A procedure based on The parameterized trajectory method as discussed above to compute rate coefficients is provided, along with a database of thermodynamic properties of the volatile compounds. The database contains electric dipole moment, polarizability, proton affinity, and ionization energy of 100 exotic volatile compounds and can be updated accordingly. Based on the parametrized trajectory method, the rates can be obtained for selected reagent ions by providing input such as CAS number, reduced electric field applied, and temperature, see Figure above.

The rate calculator provides easy and comprehensive information on effective temperature, rate coefficients, ion kinetic energy, and corresponding center-of-mass kinetic energy, see Figure below. Complete code with molecular data can be obtained from GitHub page.
This data will be useful for experimentalists to understand the type of reaction, and collision dynamics inside the PTR-MS drift tube and hence in the quantification of VOCs without instrument calibration.

However, rate coefficients computed theoretically by applying parametrized trajectory model can be verified by the experimental rate coefficients. These results rely on the accurate computation of input ingredients useful in the rate coefficient calculations. Presently, few or no experimental data for the above-mentioned properties of the molecules are available. Moreover, in the calculation of rate coefficients, theoretical assumptions may lead to results that can be different from the actual PTR-MS drift tube environment.